PHÉP CHỨNG MINH QUY NẠP
Phần lớn các định lý trong giáo trình sẽ được chứng minh bằng phương pháp quy nạp toán học :
Giả sử ta cần chứng minh một mệnh đề P(n) với n là một số nguyên không âm. Nguyên lý quy nạp toán học cho P(n) được chứng minh theo 2 bước như sau :
P (0) , và
P( n - 1) kéo theo P (n), ∀n ≥ 1.
Bước (i) được gọi là cơ sở quy nạp, bước (ii) được gọi là bước quy nạp với P(n-1) là giả thiết quy nạp.
Thí dụ 1.12 : Dùng quy nạp, chứng minh biểu thức :
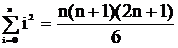
Cơ sở quy nạp : Thay n = 0 trong vế phải của biểu thức và nhận thấy cả 2 vế đều bằng 0 ⇒ P (0) luôn đúng.
Bước quy nạp : Thay n bởi n - 1 để có được giả thiết quy nạp P(n-1), sau đó tìm cách để chứng minh P(n), tức chứng minh ∀n ≥ 1, ta có :
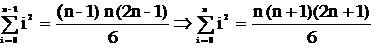
Ta có nhận xét rằng :
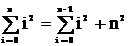
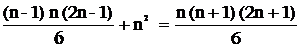
Vậy nếu ta vận dụng giả thiết quy nạp thì chỉ còn phải chứng minh biểu thức :
Với một vài phép biến đổi đại số đơn giản, biểu thức trên có thể được chứng minh dễ dàng. Hay P(n) được chứng minh, ∀n.
ĐỒ THỊ VÀ CÂY
Đồ thị (Graph)
Một đồ thị, ký hiệu G = (V, E), bao gồm một tập hữu hạn các đỉnh V (còn gọi là nút) và một tập các cạnh E nối giữa 2 nút.
Thí dụ 1.13 : Đồ thị cho bởi : V = {1, 2, 3, 4, 5}
và E = {(n, m) | n + m = 4 hoặc n + m = 7}
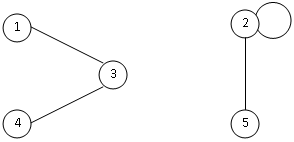
Hình 1.1 - Ví dụ về đồ thị
Một đường đi (path) trên một đồ thị là dãy các đỉnh v1, v2 , . . ., vk, k ≥ 1, sao cho trong đó có một cạnh (vi ,vi +1) cho mỗi i, 1 ≤ i < k. Độ dài của đường đi là k - 1. Nếu v1 = vk thì đường đi là một chu trình.
Chẳng hạn : 1, 3, 4 là một đường đi trong đồ thị trên.
Đồ thị có hướng (directed graph)
Một đồ thị có hướng cũng là dạng đồ thị được xác định bởi G = (V, E), trong đó V là tập các đỉnh, còn E là tập các đỉnh có thứ tự gọi là các cung (hay các đường nối có hướng giữa 2 đỉnh). Ký hiệu một cung từ v đến w có dạng v → w.
Thí dụ 1.14 : Đồ thị có hướng G = ({1, 2, 3, 4 }, { i → j | i < j })
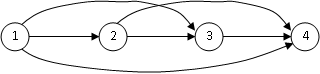
Hình 1.2 - Một đồ thị có hướng
Một đường đi trên một đồ thị có hướng là dãy các đỉnh v1, v2 , . . ., vk, k ≥ 1, sao cho với mỗi i, 1 ≤ i < k, có một cung từ vi đến vi +1. Chẳng hạn 1 → 2 → 3 → 4 là một đường đi trên đồ thị định hướng trên (từ 1 đến 4).
Cây (trees)
Cây (cây định hướng có thứ tự) là một đồ thị có hướng với các tính chất sau :
Có một nút đỉnh gọi là nút gốc
Mỗi nút còn lại đều được dẫn ra từ một nút cha ở trên nó :
- Các nút có dẫn ra nút con sau nó được gọi là nút trung gian hay nút trong.
- Các nút không dẫn ra nút con gọi là nút lá.
Thứ tự duyệt trên cây là từ trái sang phải.
Trong một cây, người ta thường dùng các khái niệm nút cha và nút con để lần lượt chỉ thứ tự trước và sau của sự phát sinh nút từ nút gốc trên cây. Nếu có một đường đi từ nút v1 đến nút v2 thì v1 được gọi là nút cha của v2 và ngược lại, v2 sẽ là nút con của nút v1.
Ta thường vẽ cây với nút gốc ở trên cùng và các cung chỉ xuống phía dưới, do vậy các ký hiệu mũi tên trở nên không còn cần thiết nữa. Các nút con của mỗi nút trên cây sẽ được vẽ lần lượt từ trái qua phải theo thứ tự đã xác định.
Thí dụ 1.15 : Cây minh họa cấu trúc cú pháp của một câu đơn trong ngôn ngữ tiếng Việt "An là sinh viên giỏi"
< Câu đơn >
< Chủ ngữ > < Vị ngữ >
< Danh từ > < Động từ > < Bổ ngữ >
< Danh từ > < Tính từ >
An là sinh viên giỏi
Hình 1.3 - Cây minh họa một câu đơn